Reducing Log File Sync Time By Increasing DML Statements Between Commits - Part 3

This page has been permanently moved. Please CLICK HERE to be redirected.

Thanks, Craig.

If you have encountered the Oracle Database wait event log file sync before, you know it can be very difficult to resolve. And even when a solution technically makes sense it can be very challenging to anticipate the performance improvement. In the first two parts of this blog series I explored the actual wait event, its common cause (rapid commits), and a very special experiment. The experiment demonstrated by increasing the inserts per commit (batching the commits) we saw quicker inserts that enabled Oracle to processes more inserts per second. We also explored the core response time performance components (service time, queue time, and arrival rate) and how they related to log file sync and our experiment. Wow... that's a lot of stuff!

In this entry I want to show you how you can visually plot the situation. This is very important for the performance analyst. First, it allows us to better communicate the situation when performance is horrible, what I call a firefighting situation (hence, the title of my associated book and training course). Second, it sets us up to understand and anticipate the impact of our proposed performance improving ideas. In this blog entry I'm going to focus on plotting the situation and in the next entry I'll introduce how to anticipate the performance change. Let's get started!

First, we need to enumericate the performance situation into the standard performance metrics of arrival rate, service time, and queue time. We have already done this (details in the previous blog entry) and the table showing some of the experimental reasults is included below (the complete table was shown in the previous blog entry, Part 2).

 Batch Arrival Rate       % Service Time       %   Queue Time       % Respone Time       %
  Size (inserts/ms)  Change (ms/inserts)  Change (ms/inserts)  Change (ms/inserts)  Change
------ ------------ ------- ------------ ------- ------------ ------- ------------ -------
     1      10.8445    0.00       0.0914    0.00       0.1356   -0.00       0.2270    0.00
     2      13.8570   27.78       0.0722  -21.01       0.1071  -20.96       0.1794  -20.98
     4      16.2470   49.82       0.0613  -32.95       0.0914  -32.61       0.1527  -32.75
     8      17.7815   63.97       0.0564  -38.34       0.0855  -36.91       0.1419  -37.49
    16      18.7664   73.05       0.0537  -41.23       0.0785  -42.11       0.1322  -41.76
    32      19.9793   84.23       0.0523  -42.76       0.0260  -80.81       0.0784  -65.48
    64      20.2438   86.67       0.0515  -43.64       0.0177  -86.92       0.0693  -69.49

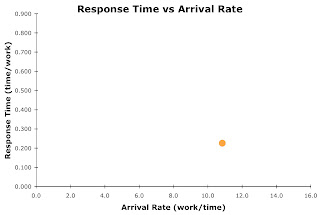
Let's plot the situation when a commit occurred immediately after each insert, that is, the batch size is only one. In this situation, the arrival rate is 10.8445 inserts/ms, the service time is 0.0914 ms/insert, and the queue time is 0.1356 ms/insert. Therefore, the response time is 0.2270 ms/insert (response time = service time + queue time).

(Now if you are used to standard response time mathematics your first question will be, "Why are we using the unit of work, insert?" The answer is because in this specific situation, inserts are highly related to the limiting performance factor, which is the inserts per commit, which manifests as a log file sync. I cover this extensively in my Advanced Oracle Performance Analysis course and it's also introduced in the last chapter of my Oracle Performance Firefighting book.)

Creating a plot with arrival rate as the horizontal axis and the response time as the vertical axis, we get an extremely boring figure like this:

I know, it's not that impressive and as they say, "It's nut'n to write home about." But it does represent the situation.... and the really cool aspect of this is, this point does reside on a response time curve. In other words, there is a response time curve that passes directly through this point. This response time curve will allow us to get a visual grasp of the situation and, as I'll present in the next blog entry, how we come up with solutions to reduce the response time per insert.

The trick is, if we can come up with a function representing the response time curve, then we can simply alter the arrival rate to let function will crank out the respective response times! So let's do it!

To determine the response time curve function, I have to introduce the basic response time formulas. Here they are along with the variable definitions:

R(io) = S / (1-(LS/M))

R(cpu) = S / ( 1 - (LS/M)^M )

Q = R - S

where:

R is response time
S is service time
L is the arrival rate
M is the number of effective CPU cores or IO devices
Q is the queue time (normally Q is the queue length, but I didn't want to add a subscript)

Yes, there are two response time formulas; one for an IO focused system and the other for a CPU focused system. In this case I am using the CPU subsystem formula because during the experiment the OS was CPU bound, not IO bound. (There is obviously much more I could say here... but I'm not.)

Most math people think the problem is pretty much a done deal at this point. Wrong! For IO focused systems you can solve for M, but for CPU focused systems, it's not going to happen. Even WolframAlpha.com won't solve M into a simple equation (take a look) . For us this means M needs to be somehow solved iteratively. There are a number of ways to do this. One way to do this is to download my Response Time Comparison spreadsheet and repeatedly try various M values converging to where the derived response time is close the experimentally observed response time. But probably the simplest method is to use a cool little web application I created, called msolve. The input form is shown below.

After a few seconds, the application returns with a solution for M. This is shown below.

It turns out that with an M of 1.4235 the derived response time closely matches are our observed response time of 0.2270 ms/insert. So we have found a good M value.

If you look closely at the bottom of the above screen shot, you'll notice a link to see the graph. If you click the link, you'll be sent to WolframAlpha.com and the graph will appear before your eyes! For this case however, I wanted the graph to look a very specific way, so I created it in MS-Excel.

To create graph in MS-Excel, keep M and S constant and varying the arrival rate (L). And there you have it, the following response time curve will appear! (I used my Response Time Comparison spreadsheet to help me create the graph.)

Now you have to admit that's pretty cool! We can now use this curve to visually show others the performance situation. But even more important, we can use the graph as the baseline (the current performance situation) to visually demonstrate how our proposed performance enhancing solutions will alter the situation to reduce the response time! In the next blog entry, I'll show you how increasing the inserts per commit will alter the response time graph so we can anticipate the impact of our solutions!

What we have done in this blog entry is to take a real Oracle system and represent it both numerically and visually. The advantage is it will help both ourselves and others better relate to the performance situation. But more importantly, it sets the stage for showing just how our proposed performance solutions will alter the situation to get us out of the elbow of the curve. This will make selling your solutions more persuasive, compelling, and truly robust.

If you're, as they say, chomping at the bit to do this kind of thing, here are some resources to help you get started:

• Download and read my paper and the associated presentation entitled, Evaluating Alternative Performance Solutions. I have presented this paper under other titles as well.
• Read the last chapter of my book, Oracle Performance Firefighting.
• Figure out how to attend my course, Advanced Oracle Performance Analysis.
• Figure out how to attend OraPub's One-Day 2010 Performance Seminar, where I introduce how to plot the curve, but don't go into all the details.

There are also other resources, but this should get you started.

Thanks for reading!

Craig.