The Average Challenge... Part 1

This page has been permanently moved. Please CLICK HERE to be redirected.

Thanks, Craig.

We have all been taught that the average of a list of numbers, is their sum divided by the count. Yes this is true, but when we rely on an average for input into a more complex formula or we use it when making an important decision what it implies and communicates becomes very important.

Why is this important?

Here are some sobering examples about why this topic is so important.

• Oracle statistics are commonly provided as an average. But as I will demonstrate (and you can validate) an average can be a poor representation of the underlying values. 
• Just because the average multiblock read takes 30ms does not mean it usually takes 30ms, yet this is how most DBAs think, talk, and act. In fact, the typical read could take only 5ms!
• Most DBAs assume that if the average log file parallel write takes 10ms, then most of the writes will center closely around 10ms and also that it is just as likely the writes will be less than 10ms than greater than 10ms...not true.
• If two different SQL statements retrieve 100 blocks from outside of Oracle's buffer cache it may take one statement 10 seconds and the other statement 2 seconds to prepare the blocks for access.
• If a SQL statement retrieves 100 blocks from outside of Oracle's buffer cache it may take one execution 10 seconds to complete while another execution only 2 seconds.

My point in this blog series is to highlight that it is important for us as performance analysts to be aware, understand, and properly use averages and also to have the ability to derive more appropriate ways to describe what's occuring. Better said, we need to use the best representation of the data to suit our performance analysis needs. If this something you are interested in, then read on!

Our Misguided Past

Suppose we look at an AWR report that shows the average log file parallel write time is 17ms. This is  validated by looking further into the report, which shows that over the AWR report interval the total log file parallel write wait time was 1200 seconds with 70,588 associated waits (the count).  What was stated and gathered is true, but from this point is where the allusions begin...

Many DBAs will make three incorrect assumptions. First, that most of the log file parallel write waits are close to 17ms and if they are not, then they are an anomaly, an outlier, and unimportant. And because they probably don't occur that often, it's nothing to be concerned about. Second, because most of us are conditioned to think of averages as part of a bell curve (i.e., normal distribution), most DBAs will envision there being just as many waits (i.e., wait occurrences) slightly less than 17ms as there are waits slightly greater than 17ms. Third, if there is a problem with using the mathematical average (i.e., mean), then everyone else is in the same boat as me and there is nothing we can realistically do anyways...so doing something about this is unusual, irrelevant, and unrealistic. All three of these assumptions are incorrect and thankfully we can address each one.

Important side note: For simplicity in this initial "average" blog entry, I am not going to use Oracle wait event times or focus on SQL statements. The reason will be clear in the subsequent blog entries. Instead I will use Oracle server and background process operating system trace output from a stressed Oracle 11.2 instance running on Linux.

The Experimental Setup

To demonstrate these assumptions and help get us thinking correctly, I created a free buffer wait load, which really stresses the IO subsystem, typically both reads and especially writes. I used a four CPU core DELL server running Oracle 11gR2 on Oracle unbreakable Linux. Here is the OS command I ran to gather the stats:

$ ps -eaf | grep lgwr
oracle   23162     1  0 Nov08 ?        00:02:30 ora_lgwr_prod18
oracle   29231 13752  0 15:11 pts/1    00:00:00 grep lgwr
$ strace -rp 23162 >lgwr_2min.trc 2>&1
$ ./crunchdata.sh lgwr_2min.trc pwrite64 mb > lgwr_2min.txt 2>&1

After two minutes, I broke out of the trace using a control-C providing me with a 1.5MB trace file with over 1000 multiblock pwrite64 system calls. I created a special shell script called crunchdata.sh to extract only the pwrite64 system call times and place this data into a single column text file. I then took the single column text file and loaded it into a pretty straightforward Mathematica notepad file to quickly crank out a nice histogram and some associated statistics. All the data shown in the blog entry and the associated analysis programs can be downloaded here.

The Results

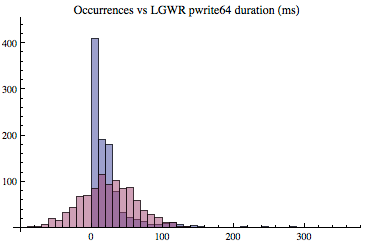
Let's first look at the histogram shown below. The horizontal axis is composed of bins, that is, groupings or intervals of how long something took, in milliseconds. For example, the far left bin is related to pwrite64 times that were between 0ms and 10ms. The second bin is related to pwrite64 times between 11ms and 20ms. And on and on. The vertical axis is the number of samples gathered, that is, the number of occurrences associated with a bin. For example, there were just over 400 pwrite64 samples whose time was between 0ms and 10ms. And while you can't see this on the graph clearly, there were 11 samples whose time was between 111ms and 120ms. If we add up all the occurrences shown in the graph it will be total the number of samples, which in this case is 1006. If you're wondering why the horizontal axis goes out to over 350ms, it's because there were some writes that actually took over 350ms and I allowed Mathematica to include all our sample data when creating the histogram. These outliers or anomalies are more important than many DBAs think and will be discussed below.

Looking at the histogram above, the first observation and the most obvious is the pwrite64 duration samples are not normally distributed. No even close! It is very skewed. To highlight this point, in the graphic below, I overlaid a normal distribution based on the same dataset's key normal distribution inputs; average and standard deviation. As you can see, the LGWR's pwrite64 times, are clearly not normally distributed.

But is this non-nomality just a convenient anomalous sample set I selected from a large number of experiments to make a point? No. To provide additional examples of this skewness, shown below are two other examples (DBWR and a server process) based on the same database server load. Each sample set was gathered like the one detailed above, except the sample time was three minutes instead of two.

The histogram below captured the database writer's 1,832 multiblock pwrite64 calls over the three minute sample period. As you can see, most of samples were between 0ms and 25ms, which is what we would hope. Also notice there were writes that took over 1400ms (1.4 seconds!) to complete. What do you think the average write time is? (The answer is provided below.)

The histogram below captured a server process's 4,019 multiblock pread64 calls over the three minute sample period. As you can see, most of samples were between 0ms and 25ms, but there was a sample just below and above 1000ms. What do you think the average read time is? (The answer is provided below.)

What's the big deal?

What's the big deal about a skewed distribution? The samples that take much longer than the rest wreak havoc on creating a meaningful and useful average. Said another way, the calculated average has an implied meaning that is not what most DBAs expect. And to demonstrate this, let's focus on the initial LGWR pwrite64 histogram. To increase clarity I modified the histogram so each bin represents a single millisecond (not 10ms as above) and I also limited the x-axis to 150ms. This allows us to effectively zoom into the area of interest. Looking at the initial and zoomed area on the below histogram, what do you think is the average write call time now? And what do you think is the most common write call duration?

Most of us would guess the average is around 15ms. Visually it seems correct. But statistically the average is 24.7ms. This may seem strange because of the large number of very short duration samples and a grouping around 20ms. The reason is there are enough longer duration samples to effectively pull the average to the right. What may be thought of as outliers or anomalies occurred often enough to significantly impact the average.

This is actually a fairly tame example. I've seen many examples where the skew is more intense and therefore the average is pulled much further to the right. So looking at the histogram directly above, would you feel comfortable stating the average is 25ms? Perhaps, but you would probably would feel much more comfortable saying the likely pwrite64 time is 15.6ms and it is highly likely the time will be less than 31.64ms. Where did I come up with these numbers and what do they mean? Read on...

What's better than the average?

In this case and as we'll see with Oracle wait times and various statistics related to SQL statements, for our purposes the average is not the most useful way to describe what happened. As I have learned with developing predictive models and communicating with others about what has actually occurred (i.e., discussing the sample data), the statistical median and other similar statistics work much better than the average.

The median is the 50th percentile value: If you ordered all the samples and selected the middle value, that would be the median and the 50th percentile value. In our LGWR two minute sample set, the median is 15.6ms, which visually seems more useful when describing our sample set than the average of 24.7ms. The 31.64ms value I wrote above is the 80th-percentile. That is, 80% of our samples are 31.64ms or less. Also, the 10%-tile is 0.5ms and the 25th%-tile is 2.0ms. Both are typically more useful than simply stating the average is 24.7ms.

There are other statistics and visualizations that can be used to describe our sample sets. I will introduce some of those in subsequent blog entries and demonstrate how to calculate the median and other percentile figures when you encounter skewed distributions. But for now, the median nearly always provides us with a better way to describe Oracle performance analysis (background and foreground processes, SQL statement resource consumption and duration) related samples.

Referring to the DBWR histogram above, the average pwrite64 took 30.2ms and the median is 1.3ms. Referring to the server process multiblock read historgram above, the average pread64 took 24.1ms and the median is a staggering 0.1ms. This common yet intense server process physical IO read time skewness has a profound impact on modeling an Oracle system providing predictive analysis. Though sometimes it is difficult to visually see without zooming into the histogram, the difference between the average and the median is because of the large sample time variation combined with a few samples that have relatively large times. But in every case, the larger the difference between average and median the more intense the skewness.

What's the point of all this?

Understanding skewness, that the average calculation is of limited value, and that the median better (among others) communicates the performance picture allows me to be more effective in my Oracle performance analysis work. More practically, when I commonly talk about an IO wait times, I try to differentiate the average wait time and the likely wait time. As as I am beginning to demonstrate, the likely wait time value will always be less than the average wait time. But how much less? And how can we calculate and predict this? These are the topics for subsequent blog entries.

This skewness actually have far reaching implications in Oracle performance analysis. I have just touched the surface and introduced the situation which, hopefully peaked your interest. As I will subsequently blog about, this skewness also occurs when analyzing Oracle wait time and in many areas of SQL statement analysis.

Thanks for reading!


Craig.

P.S. If you want me to respond to a comment or have a question, please feel free to email me directly at craig@orapub .com. I use a challenge-response spam blocker, so you'll need to open the challenge email and click on the link or I will not receive your email.